An Integrated Study of Separation Control: Flow Physics, Nonlinear Dynamics and Effective Control Strategies

Motivation

• Separated flow past an airfoil is characterized by multiple natural frequencies associated with various instabilities.

• Traditional separation control forces at a single frequency and often neglects the influence of actuator dynamics (resonance).

Questions & Objectives

• Is the effectiveness of a control strategy related to the natural flow instabilities and/or interactions?

Objective 1: Identify and analyze the various global dynamics in a separated flow configuration

• Can we detect and leverage natural instabilities to understand, model, and control separated flow in a more efficient and systematic manner?

Objective 2: Investigate the effectiveness and efficiency of targeting the instabilities in open-loop experiments

Objective 3: Apply observations to design and implement effective closed-loop control strategies

Challenges & Approach

1.     Traditional experimental methods for detection of flow frequency content are limited

-  Localized dynamic sensors (location sensitive)

-  High-rate global measurements ($$$)

Approach: Use modal analysis methods amenable to experimental techniques to obtain low-order, global estimates

2.     Characteristics of 2D flow separation on airfoils is highly dependent on angle of attack and surface curvature

Approach: A canonical flat plate model retains the essential separation characteristics, eliminates curvature effects, and is amenable to both simulations and experiments

 

 

 

 

 

 

 

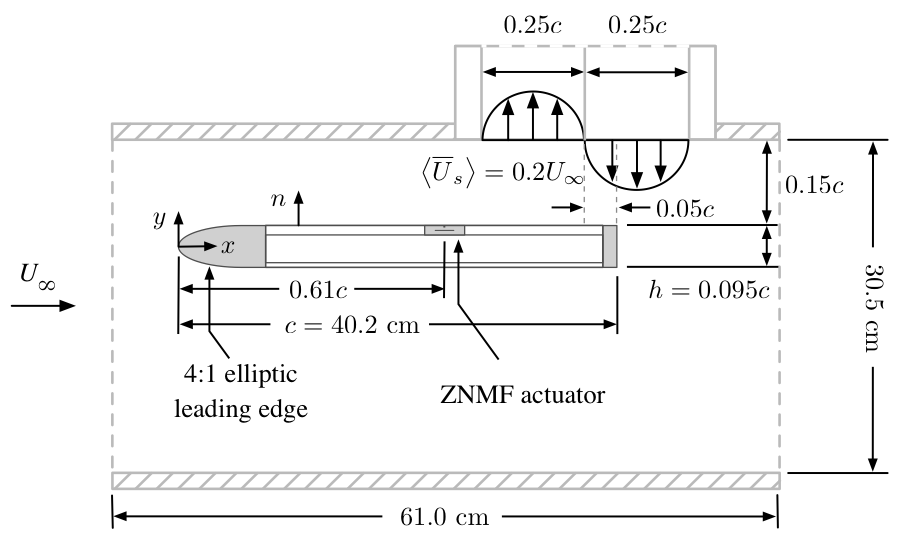
Experimental Objectives

1.     Estimate global flow dynamics (time-resolved velocity fields)

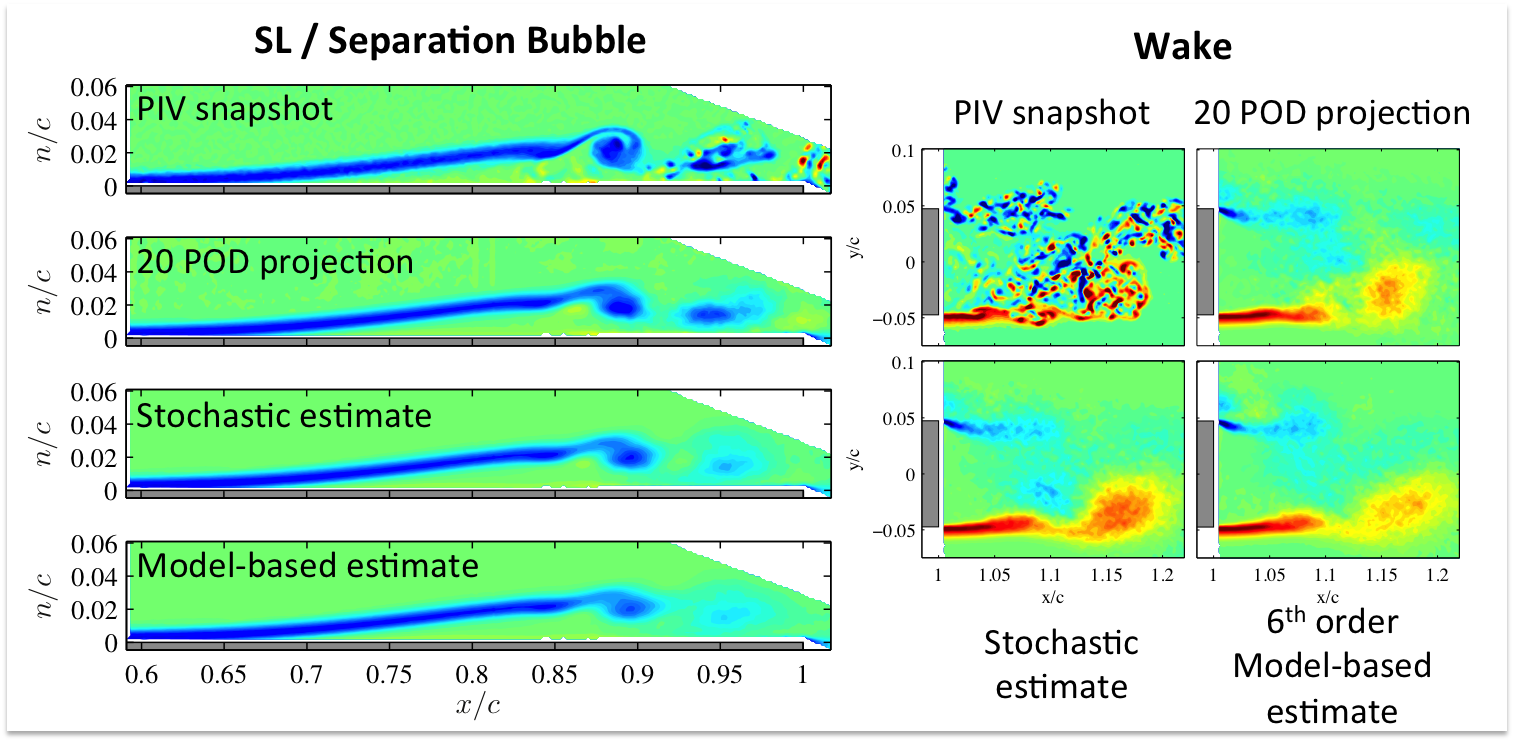
2.     Identify characteristic frequencies/instabilities

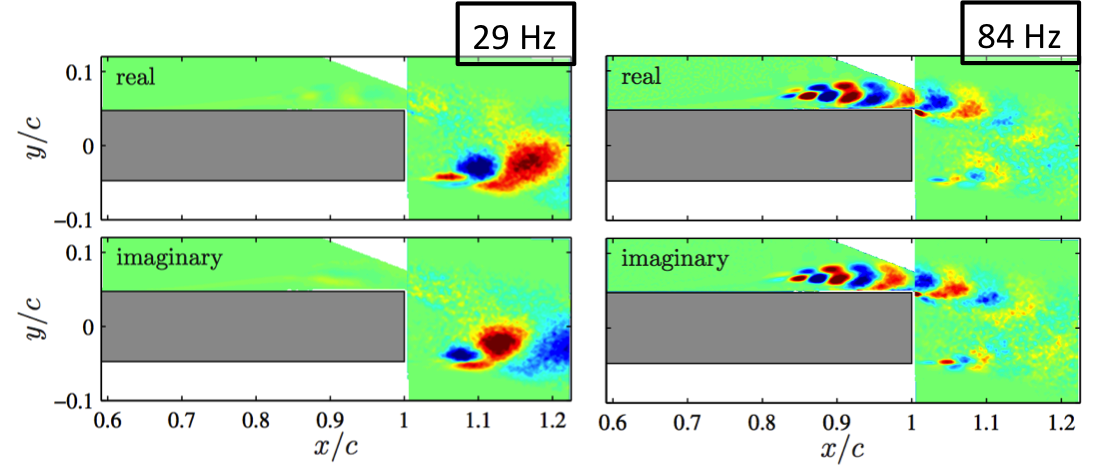
3.     Perform open-loop control

Target characteristic frequencies by modulating actuator resonance. The extent and height of the time-averaged separation bubble is reduced during control.

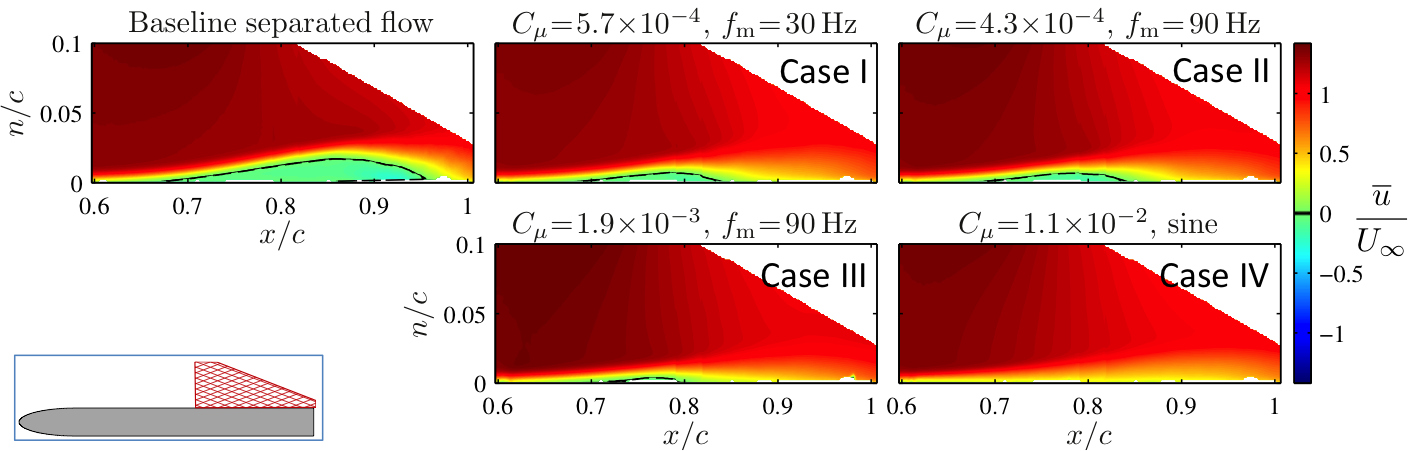
Forcing at or near the natural shear layer frequency "feeds" the characteristic roll-up of the shear layer, which increases mixing between the high-momentum freestream and the low-momentum separated flow. This ultimately reattaches the flow further upstream with little control effort, or cost, described by the coefficient of momentum C_μ.

Conclusions

• DMD extracts modal structures of the characteristic shear layer and wake components and results reveal interaction between the wake and separation bubble dynamics

• Most efficient OL control scheme targets multiple flow instabilities rather than a single instability

• CL control reattaches the flow (time average) by reducing the controlled shear layer oscillations